Подведены итоги Олимпиады по программированию среди школьников

С 16 по 22 января в Московском университете стали и сплавов прошла III Международная олимпиада по программированию среди школьников. Мероприятие было организовано НИТУ «МИСиС» и Cognitive Technologies. Признаться, понадобилось практически три недели, чтобы уговорить организаторов открыть хотя бы пару условий предложенных на мероприятии задач и получить разрешение опубликовать их разбор.

Поверьте, это было не просто. Хотя их можно понять.
Как известно, составление условий задач считается одним из наиболее сложных этапов подготовки соревнований по программированию.

По их завершению они, как правило, используются при проведении тренировок команд, а также внешних контестов.
Коллективы тренеров от разных вузов регулярно обмениваются контестами.
Вобщем, повторное использование задач принято в олимпиадном движении.

Но обо всем по порядку...

К участию в очном туре олимпиады были приглашены более 70 школьников с 8 по 11 классов из разных регионов России и Республики Беларусь, успешно выступивших в заочном туре олимпиады.
Напомним, формат мероприятия подразумевает проведение двух этапов: заочный (проводится осенью; в прошлом году он состоялся 16 ноября 2014 года; подробнее о нем можно посмотреть: ug.ru/news/13584) и очный (проводится в начале января).
Организаторы при этом отмечают, что не делают ставку на гениев и вундеркиндов из спецшкол Москвы и Санкт-Петербурга.
Целью проведения олимпиады является поиск перспективных и талантливых ребят, главным образом, из регионов России и ближнего зарубежья, желающих получить хорошее образование и реализовать себя в сфере информационных технологий.

Начиная со 2 курса обучения студенты кафедры инженерной кибернетики проходят практику в университетских лабораториях и лучшим из них предлагается принять участие в реальных научно-прикладных проектах в области ИИ реализуемых совместно с компанией Cognitive Technologies.

Очный тур олимпиады был проведен по следующим правилам.

• Продолжительность тура: 5 часов.
• Количество задач: 10.
• Рабочий язык: русский.

При ранжировании участников и выявлении победителей главным фактором являлось количество решенных задач.
При их равенстве учитывалась сумма времен от начала турнира до принятия проверяющей системой решения по всем решенным задачам плюс по 20 минут штрафа за каждое отвергнутое решение.
Штрафы за неверные решения накладывались только на те задачи, которые в конечном итоге были приняты проверяющей системой.
Для автоматизированной проверки решений использовалась система ejudge (https://ejudge.ru/).

В итоге 10 задач не решил никто.

Победителем олимпиады стал серебряный призер международной олимпиады по информатике (International Olympiad in Informatics) Алексей Вистяж из Ивьевской средней школы Республики Беларусь, который решил 9 задач.

С заметным отрывом от него (5 решенных задач) второе место поделили Александр Зойкин (Оренбург) и Юрий Бондарчук (Беларусь).

На третьем месте с четырьмя решенными задачами оказались Павел Бесчетнов (Тольяти), Дмитрий Галов (Москва) и Алексей Довгаль (Беларусь).

16 школьников, признанные победителями и призерами получили ценные призы и дополнительные баллы к общим результатам ЕГЭ при поступлении в НИТУ «МИСиС».

Наибольшую сложность вызвала задача I. «Зеркало в коридоре».
На удивление, участники плохо справились с задачами на геометрию.
Организаторы считали их относительно простыми.

Текст задачи I

Ограничение времени: 0.5 секунды
Ограничение памяти: 64 Мегабайт
Ввод: Стандартный поток ввода (stdin)
Вывод: Стандартный поток вывода (stdout)

Простуженный Петя лежал в постели, как вдруг кто-то открыл дверь. Пете было лень вставать и он посмотрел в зеркало, чтобы увидеть кто пришёл. Известны координаты вошедшего (его можно считать материальной точкой), необходимо узнать, удасться ли Пете увидеть отражение вошедшего в зеркале. Зеркало имеет форму круга с центром в начале координат и расположено в плоскости ax + by + cz = 0. Петю тоже можно считать материальной точкой. Гарантируется, что Петя и незнакомец не лежат в плоскости зеркала и что Петя всегда видит отражающую сторону зеркала. Если изображение попадает на границу зеркала, то Петя видит вошедшего. Так как и Петю и вошедшего можно считать материальными точками, Петя может увидеть отражение вошедшего как сквозь вошедшего, так и сквозь свое собственное отражение.

Исходные данные

В первой строке записано натуральное число n – количество тестов, не превышающее 500. Каждый тест состоит из четырёх строк. В первой из них записан радиус зеркала. Во второй – коэффициенты a, b, c. Далее следуют координаты Пети. В четвёртой строке каждого теста записаны координаты вошедшего. Все числа целые и по модулю не превосходят 1000.

Результат

Выведите n строк. В каждой строке – ответ на очередной тест. “Yes”, если Петя видит вошедшего и “No” в противном случае.

Разбор задачи I «Зеркало в коридоре»

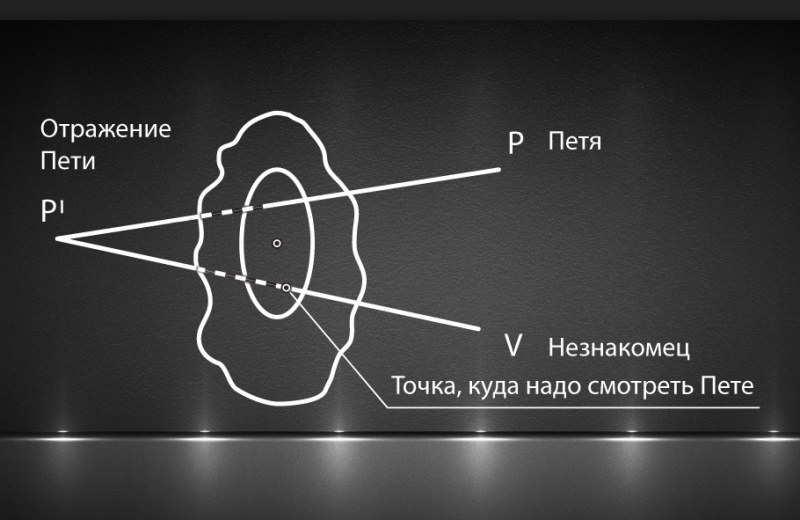
Отразим Петю относительно плоскости зеркала.
Проведём прямую через отражённого Петю и незнакомца и пересечём её с плоскостью зеркала. Посмотрим, попадает ли точка пересечения в зеркало. Отдельно рассмотрим случай, когда Петя и незнакомец лежат по разные стороны от зеркала – тогда Петя его точно не видит.

Текст задачи H «Ось симметрии»

Ограничение времени: 1 секунда
Ограничение памяти: 64 Мегабайт
Ввод: Стандартный поток ввода (stdin)
Вывод: Стандартный поток вывода (stdout)

Друзья привезли из путешествия по Китаю Вове в подарок набор для изготовления воздушного змея.
На следующий день выдалась хорошая погода, и он решил склеить змея и запустить его.
Инструкция по изготовлению, конечно, была только на китайском языке, поэтому Вова решил, что разберётся и без неё.
Немного повозившись, он соорудил змея в форме плоского многоугольника, оставалось только приклеить к нему хвост.
И тут Вове пришлось задуматься над тем, к какой точке границы многоугольника должен быть приклеен хвост змея.
Интуиция подсказала ему, что для того, чтобы полёт змея был устойчивым, его хвост должен лежать на некоторой оси симметрии многоугольника.

На рисунках ниже изображены два воздушных змея, летающих устойчиво и все варианты прикрепления к ним хвоста,
а также один воздушный змей, летающий неустойчиво.


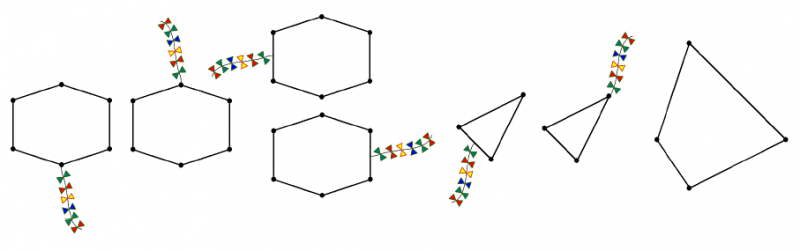
Сколько существует точек на границе многоугольника, таких что, если приклеить к ним хвост, в результате получится воздушный змей, летающий устойчиво?

Исходные данные

В первой строке записано единственное целое число N (3 ≤ N ≤ 1000). В следующих N строках записаны через пробел по два целых числа, не превосходящие по модулю 10000 – координаты вершин многоугольника в порядке обхода.

Результат

Вывести единственное число – количество точек на границе многоугольника, к которым можно приклеить хвост змея.

Разбор задачи H «Ось симметрии»

Ось симметрии многоугольника может проходить только через его вершины и через середины его сторон.
Выпишем координаты 2N точек – вершин многоугольника и середин его сторон в порядке обхода и занумеруем их от 0 до 2N-1.
Рассмотрим все претенденты на ось симметрии – прямые, проходящие через точки i и i+N, 0 ≤ i ≤ N-1.
Для того, чтобы такая прямая была осью симметрии многоугольника, необходимо и достаточно, чтобы каждая пара точек i+j и (i-j)mod 2N, 1 ≤ j ≤ N-1, была расположена симметрично относительно этой прямой.

Проверить симметричность расположения точек C и D относительно прямой AB проще всего, установив, что прямые AB и CD ортогональны и точка их пересечения делит отрезок CD пополам.
Чтобы не выходить за пределы вычисления с целыми числами, достаточно все координаты точек увеличить в 4 раза.
Трудоемкость такого решения равна O(N2).

С задачей H «Ось симметрии» справилось двое участников А.Вистяж и П.Бесчетнов.

Зимняя школа

Во время очного тура для ребят также проводилась зимняя школа программирования.

В ее рамках участникам олимпиады известные ученые и специалисты по ИТ читали лекции, проводили мастер-классы и учебно-тренировочные контесты.
Участие в зимней школе и очном туре олимпиады по программированию было бесплатным для приглашенных участников. Им обеспечивался трансфер, питание и проживание.
Каждого участника встречали на вокзале и провожали до места проведения мероприятий. На все время пребывания, со школьниками работали профессиональные вожатые, прошедшие подготовку в школе вожатых организуемой туристической компанией «ОСТ-ВЕСТ».

Задачи и тесты для очного тура олимпиады разрабатывал коллектив тренеров по спортивному программированию НИТУ «МИСиС» и Cognitive Technologies во главе с членом-корр. РАН В.Л. Арлазаровым. В их числе: к.ф.-м.н. И.А. Фараджев, к.т.н. В.В. Постников, к.ф.-м.н. И.Б. Мамай, В.В. Соколов. А также аспиранты НИТУ «МИСиС»: К.Булатов, Т.Чернов и Н.Скорюкина.

Источник: Habrahabr.ru